백지에서 시작하는 델타 시그마 DAC
디지털 음원이나 스트리밍 음원을 즐기는 애호가들이라면 반드시 만나게 되는 개념 혹은 부품이 있다. 바로 델타 시그마 DAC(Delta-Sigma Digital Analog Converter)이다. DAC이 ‘입력된 디지털 신호를 아날로그 신호로 바꿔주는 부품 혹은 오디오 기기’라고 대충 이해해도 오디오를 즐기는 데는 아무런 문제가 없다.
하지만 이 정도 상식 갖고서는 ‘오버샘플링' ‘노이즈 셰이핑' ‘로우 패스 필터' ‘비트 스트림' 같은 델타 시그마 DAC 관련 용어는 그야말로 안드로메다 외계어가 되고 만다. 무엇보다 델타 시그마 DAC의 작동원리를 모르면 요즘 인기 높은 R-2R DAC과 비교는 그냥 불가다. [하제알](하나라도 제대로 알자) 칼럼 3번째 주제로 이 델타 시그마 DAC을 정한 이유다.
0. 타임 도메인, 주파수 도메인
먼저 확실히 짚고 넘어가야 할 것이 있다. 바로 타임 도메인(Time Domain)과 주파수 도메인(Frequency Domain) 개념이다. 필자 역시 이를 혼동한 탓에 수많은 오해와 시행착오를 거쳐야 했다.
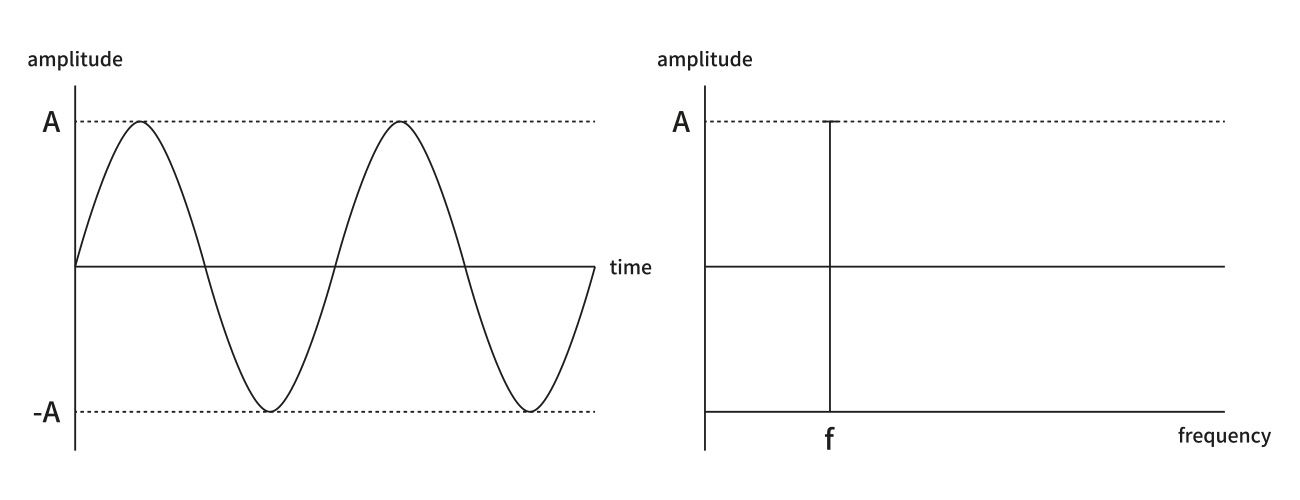
타임 도메인은 위 그림의 왼쪽 그래프처럼 특정 신호를 '시간 흐름'에서 파악하는 것이다. 때문에 가로축이 시간이고 세로축은 통상 +, - 전압(V)이다. 예를 들어 타임 도메인에서 특정 신호는 0V, 5V, 0V, -5V, 0V, 이런 식으로 변한다.
이에 비해 주파수 도메인은 오른쪽 그래프처럼 시간 흐름과 상관없이 입력되는 특정 신호의 전압(V)만을 파악한다. 예를 들어 1kHz 주파수의 5V 신호가 들어오면 주파수 도메인에서는 가로축의 1kHz 지점에서 5V 높이를 갖는 펄스(Pulse) 형태로 나타난다. 만약 2kHz에서도 뭔가 다른 펄스가 나타난다면 이는 1kHz 신호와는 상관없는 '노이즈'(noise)다.
1. 전체 흐름도 :
PCM ⇒ 업샘플링(인터폴레이션 필터) ⇒
델타 시그마 모듈레이터 ⇒ 비트스트림 ⇒ 1비트 DAC ⇒
로우패스 아날로그 필터 ⇒ 아날로그 신호
다음은 필자가 지금까지 찾아본 델타 시그마 DAC 관련 자료 중에서 가장 일목요연한 흐름도다. 델타 시그마 DAC 칩으로 유명한 미국 아날로그 디바이 시스(Analog Devices)가 공개한 블록 다이아그램이다.
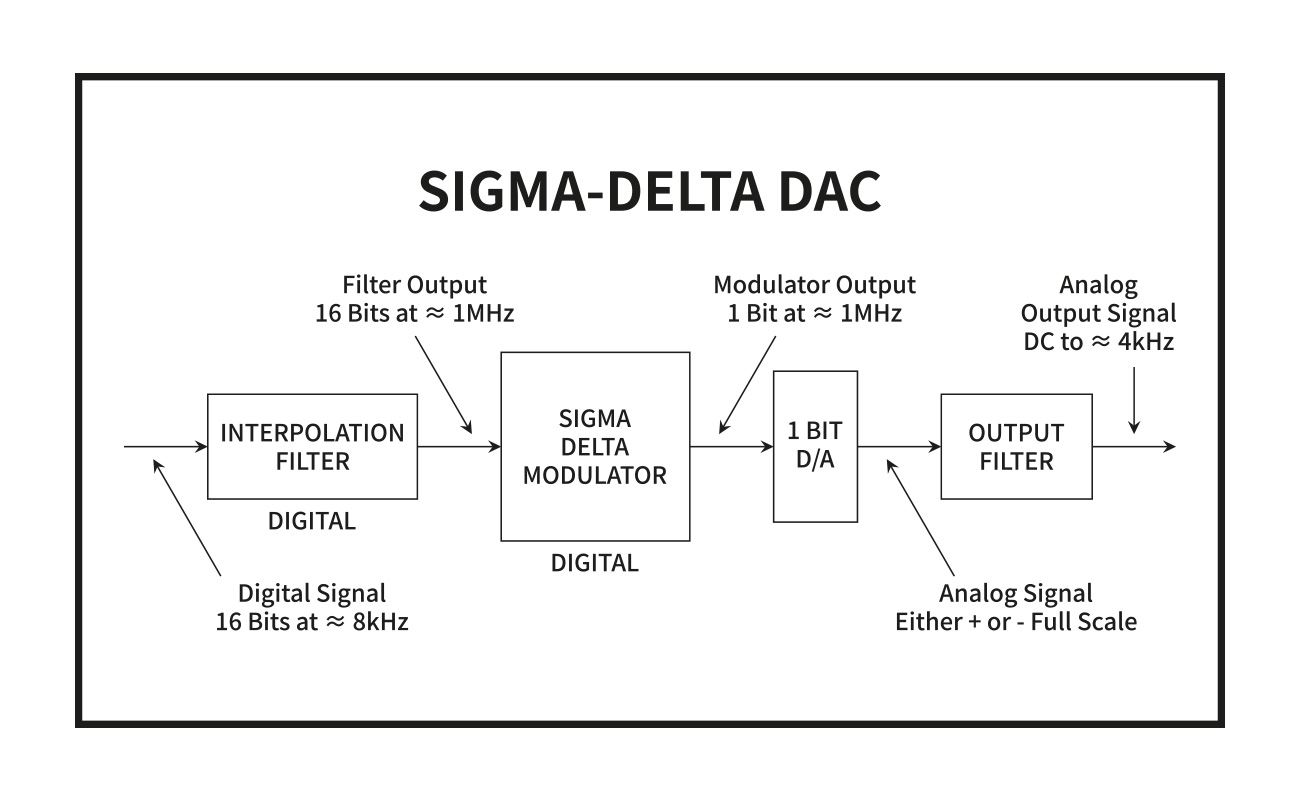
1) 타임 도메인에서 바라봤을 때 전압 값이 수시로 변하는 멀티 비트 PCM(Pulse Code Modulation) 디지털 신호가 들어온다. 자세히 보면 비트는 16비트, 샘플 레이트는 8kHz 임을 알 수 있다.
2) 인터폴레이션 필터(Interpolation Filter)에서 오버 샘플링(Oversampling)을 한다. 자세히 보면 비트는 그대로 16비트인 상태에서 샘플 레이트만 1MHz로 높아진 것을 알 수 있다. 그래서 '오버' 샘플링이다. 이렇게 오버 샘플링을 하는 이유는 입력 PCM에 끼어 들어간 양자화 노이즈(Quantization Noise)를 없애기 위한 사전 포석이다. 사후 포석은 디지털 노이즈 셰이핑(Noise Shaping)과 디지털/아날로그 로우 패스 필터(Low-Pass Filter)가 한다.
3) 오버샘플링이 이뤄진 멀티 비트 PCM 신호가 델타 시그마 모듈레이터(Delta Sigma Modulator)로 들어온다. 델타 시그마 모듈레이터 안에 노이즈 셰이핑 과정이 포함된다.
4) 델타 시그마 모듈레이터는 1비트 신호인 비트스트림(Bitstream) 디지털 신호를 출력한다. 자세히 보면 비트스트림 신호는 여전히 오버샘플링 된 1MHz 샘플 레이트를 유지하고 있는 것을 알 수 있다.
5) 1비트 DAC이 비트스트림 디지털 신호를 아날로그 신호로 바꿔준다.
6) 이렇게 얻어진 아날로그 신호는 최종적으로 저항(R)과 커패시터(C)로 이뤄진 아날로그 로우패스 필터를 통과한다. 오버샘플링 과정에서 동원된 고주파 샘플링 주파수를 최종적으로 걸러내기 위해서다. 자세히 보면 최종 출력된 아날로그 신호의 최고 주파수가 당초 샘플 레이트의 절반인 4kHz인 것을 알 수 있다. 처음 샘플 레이트가 8kHz였던 것은 샘플 레이트는 신호의 최고 주파수보다 최소 2배여야 한다는 나이퀴스트 이론(Nyquist Theorem) 때문이다.
2. 오버샘플링
PCM 신호는 샘플 레이트(sample rate)가 기준점이다. 흔히 '16비트, 44.1kHz PCM 신호'라고 말할 때의 44.1kHz가 샘플 레이트인데, 1Hz 아날로그 신호를 디지털 신호로 바꿀 때 1초 동안 4만 4100번이나 해당 전압을 잰다는 것이다. 물론 이는 타임 도메인에서 바라봤을 때다. 그런데 문제는 44.1kHz가 가청 영역대 최고 주파수(20kHz)를 2배 이상 벗어나 있긴 하지만 엄연한 고주파 노이즈라는 사실이다. 즉, 아날로그 신호에서 디지털 PCM 신호를 만들다 인위적으로 생겨난 노이즈라는 것이고, 이것이 바로 양자화 노이즈(Quantization Noise)다.
오버 샘플링(Oversampling)은 이처럼 PCM 신호가 태생적으로 가질 수밖에 없는 양자화 노이즈를 줄이기 위한 과정이다. 위에서 예를 든 8kHz 샘플 레이트가 오버 샘플링을 거쳐 1MHz가 되었다면 이는 정확히 125배 오버 샘플링을 했다는 얘기다. 즉, 8000개의 '원 샘플 사이 사이에' 샘플을 또 추가해 총 100만개의 샘플(기준점)을 만든 것이기 때문에 이를 '인터폴레이션 필터'(Interpolation Filter. 보간 필터)라고 부른다. 폴대 사이사이에 또 다른 폴대를 집어넣는 이미지라고 생각하면 된다.
여기서 심각한 궁금증이 하나 들 것이다. 샘플 레이트 주파수를 늘리는 것, 예를 들어 8배, 16배, 125배 늘리는 것이 왜 양자화 노이즈를 줄이는 사전 포석이 될까. 이는 주파수 도메인에서 바라볼 때, 정사각형 모양의 양자화 노이즈를 가로변(주파수)이 길고 세로변(전압)이 짧은 직사각형 모양의 양자화 노이즈로 바꿔주는 과정이라고 생각하면 된다. 이를 알기 쉽게 표현한 그림은 다음과 같다.
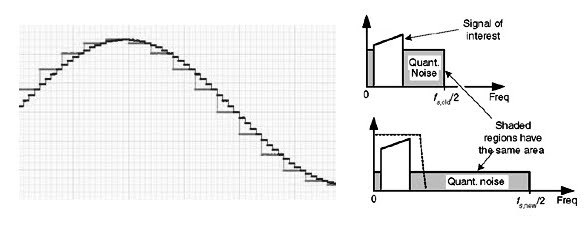
위 그림에서 왼쪽 그래프는 타임 도메인에서 바라본 오버샘플링 과정이고, 오른쪽 그래프는 주파수 도메인에서 바라본 오버 샘플링과 이에 따른 양자화 노이즈의 변화를 보여준다. 자세히 보면, 커터 칼날 모양의 음악신호에 끼어있던 양자화 노이즈가 오버 샘플링 후 키는 낮아지고 옆으로 길어진 것을 알 수 있다. 이렇게 양자화 노이즈를 옆으로 늘린 후에 특정 주파수에서 컷오프를 시키면(디지털 로우 패스 필터), 양자화 노이즈 대부분이 사라진다는 것이 오버샘플링의 논리다.
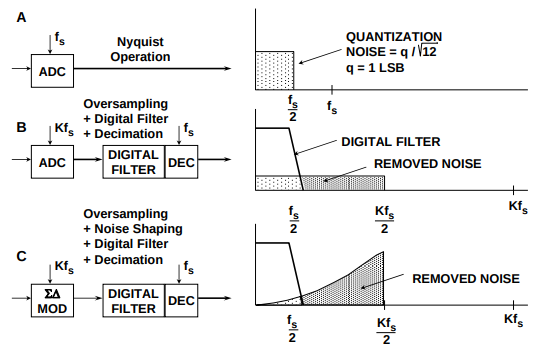
노이즈 셰이핑(Noise Shaping)은 디지털 로우 패스 필터를 통과한 양자화 노이즈를 조금이라도 더 줄이기 위한 과정이다. 위에서 3번째 그림이 노이즈 셰이핑인데, 자세히 보면 오버 샘플링과 디지털 로우 패스 필터에서 살아남은 양자화 노이즈(B 그림)가 노이즈 셰이핑을 거친 후 그 양이 대폭 줄어든 것(C 그림)을 알 수 있다. 그리고 이 노이즈 셰이핑이 이뤄지는 곳이 바로 델타 시그마 모듈레이터다.
3. 델타 시그마 모듈레이터
오버 샘플링 된 멀티 비트 PCM 신호는 드디어 델타 시그마 모듈레이터(Delta-Sigma Modulator)를 만난다. 동어반복 같지만 이 델타 시그마 모듈레이터가 있어서 델타 시그마 DAC이다.
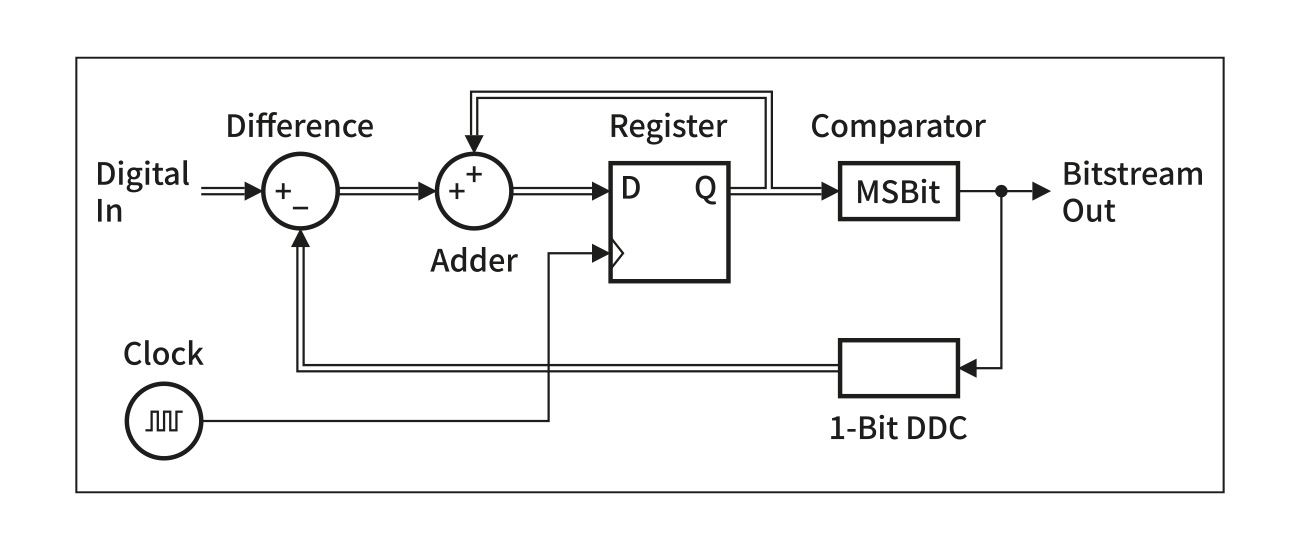
위 블록 다이아그램이 델타 시그마 모듈레이터다. 델타 시그마 모듈레이터는 DAC은 물론이거니와 ADC에서도 사용되는데, 위 다이아그램은 입력신호가 디지털 신호(Digital In)이기 때문에 DAC에 투입된 델타 시그마 모듈레이터다. 자세히 보면, 델타 시그마 모듈레이터는 감산기(Difference. 델타), 가산기(Adder. 시그마), 레지스터(Register), 비교기(Comparator), 1비트 DDC(1-Bit DDC)로 구성된 것을 알 수 있다. 그리고 1비트 DDC가 일종의 네거티브 피드백 회로를 구성해 처음 델타 연산기(감산기)로 되먹임 동작을 하고 있는데, 이 되먹임 동작이야말로 델타 시그마 모듈레이터의 핵심 중의 핵심이다.
어쨌든, 사전을 찾아보면, 델타(Delta)는 ‘변화값'이고, 시그마(Sigma)는 ‘합계'다. 개인적으로는, 이 생소하고 어렵기만 했던 델타와 시그마 개념은 ADC에 투입된 델타 시그마 모듈레이터에서 보다 확실하게 파악할 수 있었다. 델타 시그마 모듈레이터는 DAC뿐만 아니라 ADC, 즉 아날로그 디지털 컨버터에서도 쓸 수 있다. 서로 역순으로 연산을 진행하면 되기 때문이다.
예를 들어 아날로그 입력값(X)이 45이고 델타 시그마 모듈레이터를 쓴 ADC가 있다고 가정하자. 이때 델타-시그마 연산은 다음처럼 이뤄진다.
1번 연산 : X가 32보다 크거나 같은가 ⇒ 그렇다(1) ⇒ 32를 유지한다(델타)
2번 연산 : X가 48(32 + 16. 시그마)보다 크거나 같은가 ⇒ 아니다(0) ⇒ 16을 버린다(델타)
3번 연산 : X가 40(32 + 8. 시그마)보다 크거나 같은가 ⇒ 그렇다(1) ⇒ 8을 유지한다(델타)
4번 연산 : X가 44(32 + 8 + 4. 시그마)보다 크거나 같은가 ⇒ 그렇다(1) ⇒ 4를 유지한다(델타)
5번 연산 : X가 46(32 + 8 + 4 + 2. 시그마)보다 크거나 같은가 ⇒ 아니다(0) ⇒ 2를 버린다(델타)
6번 연산 : X가 45(32 + 8 + 4 + 1. 시그마)보다 크거나 같은가 ⇒ 그렇다(1) ⇒ 1을 유지한다(델타)
자세히 보면, 2번 연산에서 16을 버리라고 하니까, 다음 3번 연산에서 16이 사라진 상태에서 더하는 것을 알 수 있다. 마찬가지로 5번 연산에서 2를 버리라고 하니까, 다음 6번 연산에서 2가 사라진 상태에서 앞선 숫자들을 더하는 것을 알 수 있다. 어쨌든, 최종 결과는 이렇다.
X = 32 + 8 + 4 + 1 = 45 = 101101
여기서 ‘32 + 8 + 4 + 1’은 델타 명령(유지하라, 버려라)에 따른 최종 시그마 합계이고, ‘101101’은 1~6번 연산 때마다 출력된 1비트 신호값이다. 결국 델타는 처음 입력 신호에서 변화량을 ‘빼는’는 연산이고(감산기), 시그마는 앞에서 나온 델타 연산값에 이전 값을 ‘더하는' 연산이다(가산기). 그리고 ‘이전 값'을 잠시 등록/저장해두는 것이 레지스터(Register), ‘네/아니오’ 2가지 답만 할 수 있는 질문장치가 비교기, 즉 컴패레이터(Comparator)다.
델타 시그마 모듈레이터를 채택한 DAC 역시 멀티 비트의 PCM 디지털 신호가 들어오면, 컴패레이터 ⇒ 델타 연산 ⇒ 시그마 연산을 N 차례 반복해 최종 1비트 비트스트림 디지털 신호를 출력하는 과정이라고 생각하면 된다. 그리고 이 같은 연산을 몇 번(N) 하는가, 처음 컴패레이터의 기준값(위에서는 32)을 얼마로 할 것인가는 해당 DAC에 들어오는 데이터(신호)의 비트 수에 달렸다. 예를 들어 6비트 데이터가 들어오면 총 연산 회수가 6차례, 컴패레이터 기준값은 2의 5승값인 32가 된다. 16비트 데이터라면 16차례, 2의 15승값인 32,768이 기준값이 된다.
예를 들어 8비트 데이터의 PCM 신호가 들어온다고 가정해보자. 잘 아시는 대로 컴퓨터에 저장되는 데이터의 최소 단위는 1바이트(8비트)이고 8비트 신호의 최솟값~최댓값을 2진법으로 표기하면 00000000~11111111이다. 이를 보다 자주 쓰이는 16진법(Hexadecimal)으로 표기하면 0x00~0xff다. 이때 컴패레이터의 기준값은 2의 7승 값인 128이 된다. 8비트 신호이기 때문이다. 128을 16진법으로 표기하면 0x80이기 때문에, 델타 시그마 DAC의 컴패레이터 첫 번째 연산은 다음 2가지 경우밖에 없다.
1) X가 0x80보다 크거나 같은가? ⇒ 그렇다 : 컴패레이터에서 1 출력 ⇒ DDC에서 0xff 출력 ⇒ 델타 연산기에 0xff 입력 ⇒ 이 결괏값을 시그마 연산기에 입력 ⇒ 다음 단계
2) X가 0x80보다 크거나 같은가? ⇒ 아니다 : 컴패레이터에서 0 출력 ⇒ DDC에서 0x00 출력 ⇒ 델타 연산기에 0x00 입력 ⇒ 이 결괏값을 시그마 연산기에 입력 ⇒ 다음 단계
4. 비트스트림
ADC가 됐든 DAC이 됐든 델타 시그마 모듈레이터는 위의 경우처럼 출력값이 '101101'처럼 나오는 것이 핵심이다. 이것이 바로 비트스트림(Bitstream)이다. 전압 값이 하이(1)와 로우(0)로만 이뤄진 1비트 신호로 구성됐다는 뜻이다. 이에 비해 16비트 PCM은 하이와 로우 사이에 총 3만2768단계(2의 15승), 24비트 PCM은 총 838만8608단계(2의 23승) 차이가 나는 신호다.
백문이 불여일견. 델타 시그마 모듈레이터에서 출력된 비트스트림은 이렇게 생겼다. 맨 아래 그림(PPM Pulse)이다.
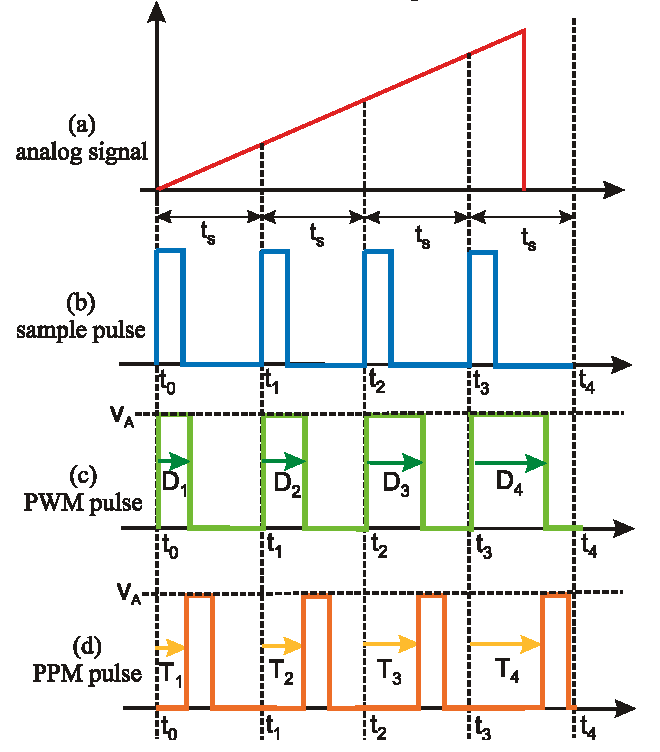
언뜻 보면 비트스트림 PPM 신호는 PWM 신호와 비슷하지만 다르다. PWM(Pulse Width Modulation. 펄스 폭 변조) 신호는 펄스 폭(width)이 변하지만, PPM(Pulse Position Modulation. 펄스 위치 변조)는 펄스 폭은 똑같고 위치(position)가 변한다. 위 그림에서 보자면, PWM 신호는 폭(D1~D4)이 다르고, PPM 신호는 펄스가 시작되는 시간(T1~T4)이 다르다. 위치가 펄스마다 다른 것이다.
하지만 필자가 보기에 결과값이 PWM 형태인지, PPM 형태인지는 어차피 곁가지다. 핵심은 델타 시그마 모듈레이터는 입력된 하이 비트(High Bit), 로우 샘플 레이트(Low Sample Rate) PCM 신호가 1비트 비트스트림이라는 로우 비트(Low Bit), 하이 샘플 레이트(High Sample Rate) 신호로 바뀐다는 것이다.
예를 들어 16비트, 44.1kHz 샘플 레이트의 PCM 신호가 델타 시그마 모듈레이터를 통과하면 예를 들어 1비트, 5644.8kHz 샘플 레이트의 비트스트림으로 바뀌는 것이다. 그리고 이 로우 샘플 레이트를 하이 샘플레이트로 바꾸는 동작이 오버 샘플링이다. 5644.8kHz는 44.1kHz를 정확히 128배 오버 샘플링한 것이다.
5. 1비트 DAC
이제 몇 단계밖에 남지 않았다. 먼저 드는 질문은 이것이다. '델타 시그마 모듈레이터를 통해 얻은 비트스트림 신호를 결국 아날로그 신호로 바꿔주는 것은 무엇인가?'. 이 일을 맡는 것이 바로 1비트 DAC이다. 출력 아날로그 전압값이 2종류밖에 없어서 1비트 DAC이다. 예를 들어 다음과 같은 비트스트림 신호가 +5Vcc와 0V만 출력하는 1비트 DAC에 입력되면 다음과 같은 아날로그 전압이 출력된다.
00 ⇒ 0/4 x 5V = 0V
01 ⇒ ¼ x 5V = 1.25V
10 ⇒ 2/4 x 5V = 2.5V
11 ⇒ ¾ x 5V = 3.75V
자세히 보면 입력되는 4개 비트스트림마다 전압이 정확히 1.25V씩 차이가 난다. 그리고 00, 01, 10, 11이라는 신호는 '주파수 도메인'에서 바라봤을 때 4개 펄스에 다름이 아니다. 이번에는 다음과 같은 비트스트림 신호가 들어온다고 했을 때 경우의 수다. 1비트 DAC은 위에서와 마찬가지로 +5Vcc 또는 0V만 출력할 수 있다.
000 ⇒ 0/8 x 5V = 0V
001 ⇒ ⅛ x 5V = 0.625V
010 ⇒ 2/8 x 5V = 1.25V
011 ⇒ ⅜ x 5V = 1.875V
100 ⇒ 4/8 x 5V = 2.5V
101 ⇒ ⅝ x 5V = 3.125V
110 ⇒ 6/8 x 5V = 3.75V
111 ⇒ ⅞ x 5V = 4.375V
8가지 비트스트림마다 출력 전압이 정확히 0.625V씩 차이가 난다. 2자리수 비트스트림 신호 때보다 출력 전압 차이가 보다 촘촘해졌다. 따라서 비트 스트림의 자리수가 늘어날수록 각각 출력되는 아날로그 신호의 전압 차이는 더욱 줄어들 것이 100% 확실하다.
6. 아날로그 로우패스 필터
양자화 노이즈는 위에서 살펴봤듯이 이미 디지털 필터를 통해 컷 오프 되었지만 한 번 더 필터링 과정을 거친다. 바로 저항(R)과 커패시터(C)로 이뤄진 아날로그 로우패스(Low-Pass) 회로다.
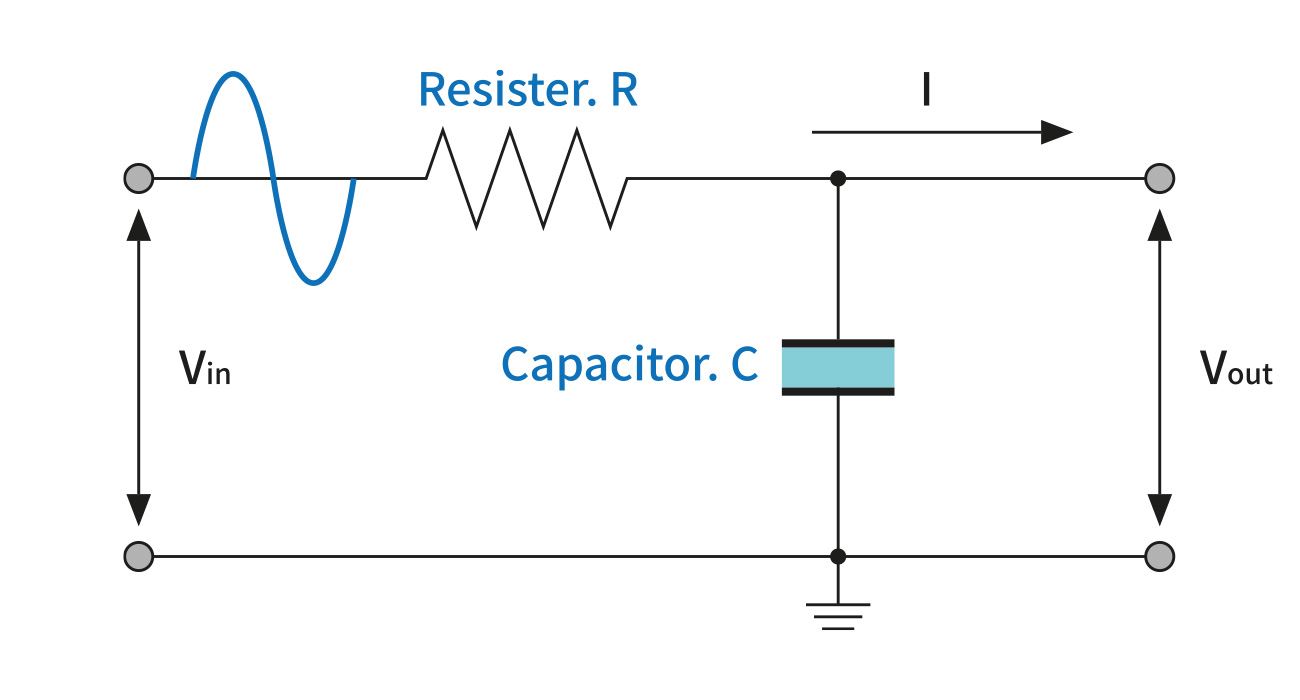
자세히 보면 아날로그 신호는 곧바로 저항을 통과하고, 이후에 오는 커패시터는 그라운드에 연결된 것을 알 수 있다. 커패시터는 잘 아시는 대로 직류(DC) 차단, 하이패스(High-Pass) 필터다. 때문에 DAC을 통과한 아날로그 신호에 남아있는 고주파 양자화 노이즈는 커패시터를 통과해(하이패스) 그라운드로 빨려 들어가고 최종 출력 신호는 결과적으로 로우패스 신호가 된다. 마침내 양자화 노이즈까지 대폭 삭감된 아날로그 원신호가 델타 시그마 DAC으로 얻어진 것이다.


